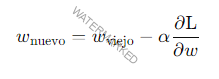Retropropagación o backpropagation es un algoritmo fundamental utilizado en el entrenamiento de redes neuronales artificiales.
Fue popularizado en la década de 1980 por Geoffrey Hinton y otros investigadores.
Su desarrollo permitió el avance de las redes neuronales profundas modernas.
La retropropagación facilita el ajuste de los pesos de las conexiones dentro de una red neuronal.
Para minimizar el error entre las predicciones del modelo y las etiquetas reales.
Utilizando el cálculo del gradiente.
¿Qué es y cómo funciona?
En una red neuronal, el objetivo es ajustar los pesos de las conexiones entre neuronas.
De manera que la salida de la red se acerque lo más posible a los resultados esperados.
El algoritmo de retropropagación realiza los siguientes pasos en un ciclo iterativo.
Forward pass (paso hacia adelante)
La entrada se pasa a través de la red, capa por capa, hasta que se obtiene una predicción o salida final.
Las activaciones de cada neurona se calculan usando una función de activación.
Como la sigmoide, ReLU, etc. y las conexiones entre las neuronas están ponderadas.
Por valores que se ajustarán durante el entrenamiento.
En este punto, se compara la salida de la red con la salida deseada (verdadero valor o etiqueta).
Para calcular el error o la pérdida usando una función de pérdida.
Como el error cuadrático medio o la entropía cruzada.
Cálculo del error
El error mide qué tan lejos está la salida de la red de los resultados deseados.
Cuanto mayor sea el error, mayor será la diferencia entre la predicción y la realidad.
El objetivo es minimizar esta función de error.
Backward pass (paso hacia atrás)
La retropropagación es el proceso de ajustar los pesos de la red neuronal utilizando el gradiente del error con respecto a cada peso.
Esto se hace calculando la derivada de la función de pérdida con respecto a los pesos de la red.
Indica en qué dirección y en qué magnitud deben ajustarse los pesos para reducir el error.
Se utiliza el algoritmo de descenso por gradiente para actualizar los pesos.
Los gradientes de error se propagan hacia atrás desde la capa de salida.
Hacia las capas anteriores (de ahí el nombre retropropagación).
Actualización de pesos
-
- Cada peso se ajusta según la magnitud del gradiente calculado en el paso anterior. Este ajuste es proporcional a una tasa de aprendizaje (α\alphaα), un hiperparámetro que controla el tamaño de los pasos con los que se actualizan los pesos:
-
- wviejow_{\text{viejo}}wviejo es el valor actual del peso.
-
- α\alphaα es la tasa de aprendizaje.
-
- ∂L∂w\frac{\partial \text{L}}{\partial w}∂w∂L es el gradiente de la función de pérdida con respecto al peso w.
Detalles importantes en el funcionamiento de la retropropagación
Función de activación
Las neuronas utilizan funciones de activación no lineales.
Como ReLU, sigmoide o tangente hiperbólica para transformar las entradas en salidas.
Estas funciones son importantes porque permiten a la red neuronal.
Aprender relaciones complejas y no lineales entre los datos.
Función de pérdida
Esta mide la diferencia entre la predicción de la red y la etiqueta real.
Algunas funciones de pérdida comunes son el error cuadrático medio usado en regresión.
Y la entropía cruzada usada en clasificación.
Descenso por gradiente
El algoritmo de descenso por gradiente es el mecanismo que se utiliza para ajustar los pesos.
Calcula la dirección en la que la función de pérdida disminuye más rápidamente (el gradiente negativo).
Ajusta los pesos en esa dirección para minimizar el error.
Gradiente
La retropropagación calcula el gradiente de la función de pérdida.
Con respecto a cada peso de la red usando la regla de la cadena de cálculo.
Este gradiente indica cuánto debe cambiar cada peso para minimizar el error total.
Ventajas de la retropropagación
Eficiencia
La retropropagación permite entrenar redes neuronales.
Con una gran cantidad de parámetros (pesos) de manera eficiente.
Propagando los errores hacia atrás a través de la red.
En lugar de recalcular todo el sistema desde cero en cada iteración.
Escalabilidad
Funciona bien para redes neuronales profundas, con muchas capas y millones de parámetros.
Ha sido clave en el auge de las redes neuronales profundas modernas.
Flexibilidad
Puede usarse con diversas arquitecturas de redes neuronales.
Redes neuronales convolucionales (CNN) para el procesamiento de imágenes.
Redes neuronales recurrentes (RNN) para secuencias de datos como el lenguaje natural.
Desventajas y desafíos
Desvanecimiento y explosión del gradiente
En redes muy profundas, los gradientes calculados durante la retropropagación pueden volverse extremadamente pequeños (gradiente desvanecido).
También extremadamente grandes (gradiente explosivo).
Estos problemas pueden hacer que el entrenamiento sea lento o inestable.
Algunas soluciones incluyen el uso de funciones de activación como ReLU.
Y técnicas como Batch Normalization o inicialización adecuada de pesos.
Dependencia de la tasa de aprendizaje
Elegir una tasa de aprendizaje incorrecta puede hacer que la red no converja (tasa demasiado alta).
Que el entrenamiento sea extremadamente lento (tasa demasiado baja).
Existen técnicas como el ajuste dinámico de la tasa de aprendizaje.
Y el uso de optimizadores avanzados como Adam que mitigan este problema.
Aplicaciones de la retropropagación
Reconocimiento de imágenes
La retropropagación es el núcleo del entrenamiento de redes neuronales convolucionales (CNN).
Utilizadas en tareas como el reconocimiento facial.
La clasificación de imágenes y la detección de objetos.
Procesamiento del lenguaje natural (NLP)
En tareas de traducción automática, análisis de sentimientos.
Generación de texto y otros problemas relacionados con el lenguaje.
Se entrenan redes neuronales profundas mediante retropropagación.
Predicciones financieras y de series temporales
Las redes neuronales recurrentes (RNN) y sus variantes como LSTM y GRU.
Utilizan retropropagación para aprender patrones en secuencias de datos.
La retropropagación es el algoritmo clave que hace posible entrenar redes neuronales profundas.
Ajustando los pesos de manera eficiente para minimizar el error.
Aunque tiene desafíos, como el desvanecimiento del gradiente.
Ha demostrado ser fundamental para el éxito de la inteligencia artificial moderna.
Permitiendo resolver problemas complejos en visión por computadora.
Procesamiento de lenguaje natural y muchos otros campos.