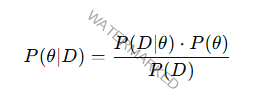Inferencia Bayesiana es un enfoque en estadística y aprendizaje automático.
Utiliza la teoría de probabilidad bayesiana.
Para actualizar nuestras creencias sobre un parámetro o hipótesis.
A medida que recibimos nueva información o datos.
En el contexto de la inteligencia artificial, la inferencia bayesiana es clave para desarrollar modelos.
qQe aprendan y ajusten sus predicciones en función de evidencia o datos observados.
Es fundamental en áreas como redes bayesianas.
Procesamiento de lenguaje natural y aprendizaje de modelos probabilísticos.
Teoría y Fundamento de la Inferencia Bayesiana
La inferencia bayesiana se basa en el Teorema de Bayes.
Describe la probabilidad de un evento o parámetro dado.
El conocimiento previo y la nueva información obtenida.
El teorema se expresa como:
P(θ∣D) P(\theta | D) P(θ∣D) es la probabilidad posterior: la probabilidad del parámetro θ\thetaθ dado los datos DDD.
P(D∣θ) P(D | \theta) P(D∣θ) es la verosimilitud: la probabilidad de observar los datos DDD si el parámetro es θ\thetaθ.
P(θ) P(\theta) P(θ) es la probabilidad previa (o simplemente “prior”) de θ\thetaθ, una creencia inicial sobre θ\thetaθ antes de observar los datos.
P(D) P(D) P(D) es la evidencia o probabilidad marginal de los datos, que actúa como un factor de normalización para que el total de probabilidades sume 1.
Componentes Clave en Inferencia Bayesiana
Distribución Priori (Prior)
Representa nuestras creencias iniciales sobre el parámetro θ\thetaθ antes de observar los datos.
Ya que afecta cómo se actualizarán las creencias una vez que se recibe la nueva información.
Si sabemos que los resultados de un experimento suelen estar en un cierto rango.
Esa información se incluirá en el prior.
Verosimilitud (Likelihood)
Mide qué tan probable es observar los datos dados ciertos valores del parámetro θ\thetaθ.
Es un componente crítico para calcular cómo cada observación influye en el ajuste de nuestras creencias sobre θ\thetaθ.
Distribución Posterior (Posterior)
Es el resultado de aplicar el Teorema de Bayes.
Combina la información del prior y la verosimilitud para dar una probabilidad ajustada de θ\thetaθ después de considerar la evidencia de los datos.
Proceso de Inferencia Bayesiana
El flujo de trabajo de inferencia bayesiana sigue estos pasos;
Definición del Prior
Seleccionamos un prior que represente nuestro conocimiento inicial.
Supuestos sobre el parámetro θ\thetaθ.
Cálculo de la Verosimilitud
Determinamos cómo se relacionan los datos DDD con θ\thetaθ, formulando un modelo probabilístico.
Aplicación del Teorema de Bayes
Combinamos el prior con la verosimilitud para obtener la distribución posterior.
Representa nuestras creencias actualizadas sobre θ\thetaθ a la luz de los datos observados.
Repetición con Nuevos Datos
Si se reciben nuevos datos, el posterior calculado previamente se convierte en el nuevo prior.
El proceso se repite para actualizar las creencias continuamente.
Ejemplo de Inferencia Bayesiana: Diagnóstico Médico
Supongamos que un médico quiere calcular la probabilidad.
De que un paciente tenga una enfermedad EEE como una infección.
Dado un resultado positivo en una prueba DDD.
Se conocen los siguientes valores;
P(E)
Probabilidad previa de la enfermedad basada en la prevalencia de la enfermedad en la población.
P(D∣E)P(D | E)P(D∣E)
Probabilidad de un resultado positivo si el paciente tiene la enfermedad.
P(D∣¬E) P(D | \neg E) P(D∣¬E)
Probabilidad de un resultado positivo si el paciente no tiene la enfermedad.
Con el teorema de Bayes, el médico puede calcular la probabilidad posterior.
P(E∣D)P(E | D)P(E∣D) indica cuán probable es que el paciente tenga la enfermedad después de un resultado positivo.
Esta actualización ayuda a reducir la incertidumbre en el diagnóstico.
En función de los datos y permite adaptar el tratamiento.
De acuerdo con las probabilidades ajustadas.
Aplicaciones de la Inferencia Bayesiana en IA
La inferencia bayesiana es ampliamente utilizada en inteligencia artificial.
Para manejar incertidumbres en varios problemas complejos.
Redes Bayesianas
Grafos probabilísticos donde los nodos representan variables.
Las conexiones representan dependencias entre estas.
Las redes bayesianas permiten modelar incertidumbres.
Calcular probabilidades condicionales.
Es útil en diagnóstico, toma de decisiones y reconocimiento de patrones.
Aprendizaje de Máquinas Probabilístico
En aprendizaje automático, los modelos bayesianos permiten actualizar creencias.
A medida que se presentan nuevos datos.
Manteniendo un enfoque probabilístico.
Captura incertidumbres y mejora la robustez de las predicciones.
Procesamiento de Lenguaje Natural (NLP)
Las técnicas bayesianas son útiles en tareas como clasificación de texto y análisis de sentimientos.
La inferencia bayesiana ayuda a modelar las probabilidades de categorías dadas.
Palabras específicas o características contextuales.
Algoritmos de Filtrado
Como el filtro de Kalman en sistemas de seguimiento.
Se estiman posiciones futuras con incertidumbres basadas en datos previos y actuales.
Optimización de Hiperparámetros: Métodos como la optimización bayesiana.
Busca el mejor conjunto de hiperparámetros para un modelo de aprendizaje automático.
Usando un enfoque bayesiano de actualización.
Exploración de nuevas combinaciones de parámetros.
Ventajas de la Inferencia Bayesiana
Incorporación de Conocimiento Previos
Permite integrar conocimiento previo en el análisis.
Haciendo posible ajustar predicciones de forma más intuitiva.
En contextos de escasa información.
Modelo de Incertidumbre Natural
Calcula de forma explícita la incertidumbre.
Facilitando decisiones más informadas.
Especialmente en situaciones críticas.
Flexibilidad y Adaptabilidad
Con la inferencia bayesiana, es posible actualizar predicciones en tiempo real.
Es útil en entornos donde los datos cambian continuamente.
Desventajas y Desafíos de la Inferencia Bayesiana
Complejidad Computacional
Calcular distribuciones posteriores en modelos complejos.
De alta dimensión puede ser costoso y lento.
Métodos como el muestreo de Monte Carlo son frecuentemente necesarios.
Pero estos también pueden aumentar la carga computacional.
Sensibilidad al Prior
La selección del prior puede influir en los resultados.
Especialmente cuando hay poca información en los datos observados.
La elección de un prior inadecuado puede sesgar los resultados.
Dificultad en la Interpretación
Para personas sin formación en estadística bayesiana.
Interpretar y seleccionar priors.
Así como entender las distribuciones posteriores, puede ser un desafío.
Métodos para Aproximar la Inferencia Bayesiana
En casos donde la posterior es complicada de calcular de manera exacta.
Existen métodos que permiten obtener aproximaciones.
Muestreo de Monte Carlo
Utiliza muestreo aleatorio para aproximar la posterior.
En situaciones donde no es posible calcularla analíticamente.
Métodos de Monte Carlo vía Cadenas de Markov (MCMC)
Genera muestras de la posterior a través de una cadena de Markov.
Permitiendo aproximar la distribución posterior.
Con más precisión en problemas complejos.
Variational Inference
Se aproxima la posterior a través de técnicas de optimización.
Buscando una distribución más sencilla que se acerque a la posterior real.
Es un enfoque rápido y escalable.
Muy útil en modelos de alta dimensión.
La Inferencia Bayesiana proporciona un marco sólido.
Para el razonamiento probabilístico en inteligencia artificial.
Permitiendo ajustar creencias sobre parámetros e hipótesis de forma iterativa.
A medida que se observa nueva información.
Su capacidad de representar y gestionar la incertidumbre la hace ideal.
Para tareas donde los datos son limitados donde la precisión es esencial.
Su complejidad computacional y su dependencia en la elección de los priors siguen siendo desafíos.
En aplicaciones más complejas o en problemas de gran escala.