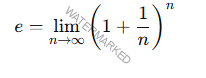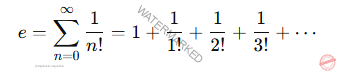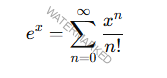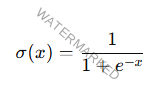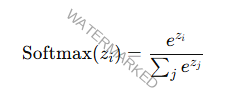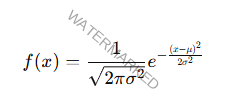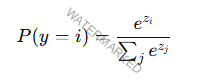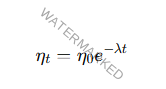Número de Euler (𝑒) es una constante matemática fundamental en matemáticas, ciencia e ingeniería.
Incluida la inteligencia artificial (IA).
Su valor es aproximadamente 2.71828
Tiene aplicaciones en áreas como cálculo, estadística.
Teoría de probabilidades y algoritmos de aprendizaje automático.
El número de Euler aparece principalmente en funciones exponenciales.
Logaritmos naturales y distribuciones estadísticas.
Son fundamentales para el desarrollo y entrenamiento.
De modelos de aprendizaje.
Propiedades Matemáticas del Número de Euler
Definición Formal
El número 𝑒 puede definirse como el límite de la siguiente expresión
Expresión de Serie
También puede representarse como una serie infinita
Relación con Funciones Exponenciales
𝑒 es la base de la función exponencial
La derivada y la integral de ex^ son ambas ex^
lo que lo hace único y fundamental en cálculo.
Aplicaciones del Número de Euler en IA
Funciones de Activación
En redes neuronales 𝑒 es esencial en funciones de activación.
Que introducen no linealidad en los modelos.
Sigmoide
Mapea los valores de entrada a un rango entre 0 y 1.
Softmax
Utilizada para probabilidades en clasificación multiclase.
Regularización y Penalización
Aparece en funciones de penalización exponencial.
En técnicas de regularización por ejemplo, L2 o dropout
Para evitar el sobreajuste.
Modelado Probabilístico
En métodos probabilísticos.
𝑒 se utiliza para expresar funciones de densidad en distribuciones.
Distribución Normal
Donde 𝑒 captura la caída exponencial.
De las probabilidades alejadas de la media.
Gradiente Descendente
En algoritmos de optimización.
La función exponencial basada en 𝑒
Se utiliza en la actualización de pesos y en funciones de costo.
Sistemas Basados en Tiempo
𝑒 modela el crecimiento y el decaimiento exponencial.
Útil en análisis de series temporales y sistemas dinámicos.
Ventajas del Uso de 𝑒 en IA
Propiedades Matemáticas Elegantes
Su comportamiento natural en derivadas e integrales.
Lo hace ideal para modelar fenómenos continuos.
Capacidad de Modelar Decaimiento
Los algoritmos que dependen de tasas de aprendizaje adaptativas.
Decaimiento exponencial por ejemplo, Annealing
Utilizan funciones basadas en 𝑒.
Compatibilidad con Probabilidades
Facilita el cálculo de probabilidades.
Debido a su uso en funciones logarítmicas y exponenciales.
Ejemplos Prácticos
Clasificación Multiclase con Softmax
En un problema de clasificación, el modelo calcula puntuaciones z para cada clase.
La función softmax, basada en 𝑒, convierte estas puntuaciones en probabilidades:
Distribuciones en Modelado Bayesiano
En un modelo bayesiano, se usan funciones exponenciales basadas en 𝑒
Para calcular probabilidades condicionales y prioris.
Reducción de Peso en Redes Neuronales
El decaimiento exponencial, como:
Se utiliza para reducir la tasa de aprendizaje (ηt) durante el entrenamiento.
El número de Euler (𝑒) es un componente esencial en muchas aplicaciones de la IA.
Debido a sus propiedades únicas en funciones exponenciales y logarítmicas.
Su capacidad para modelar crecimiento, decaimiento y relaciones no lineales.
Lo hace indispensable para algoritmos y modelos.
Que impulsan la inteligencia artificial moderna.
Te puede interesar;
Curso de ChatGPT: Todo lo que debes saber