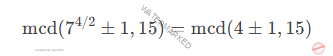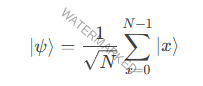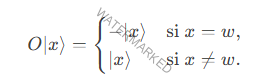Los algoritmos cuánticos más famosos: el algoritmo de Shor y el algoritmo de Grover.
Ambos son ejemplos clave de cómo la computación cuántica.
Puede superar a la computación clásica en tareas específicas.
Algoritmo de Shor
Objetivo
El algoritmo de Shor es un algoritmo cuántico.
Diseñado para factorizar números enteros grandes
En sus componentes primos.
Es importante porque la seguridad de muchos sistemas criptográficos.
Como RSA se basa en la dificultad de factorizar.
Números grandes en computadoras clásicas.
Pasos del algoritmo
El algoritmo de Shor consta de dos partes: una clásica y una cuántica.
Parte clásica:
Si el número N es par o tiene factores triviales, se devuelven esos factores.
De lo contrario, se elige un número aleatorio
a (donde 1 < a < N) y se verifica si mcd (a, N ) = 1
Si no es 1 se ha encontrado un factor.
Si mcd (a, N) = 1 se procede a la parte cuántica.
Parte cuántica:
Se utiliza un circuito cuántico para encontrar el orden r de a módulo N
El menor entero positivo r tal que ar ≡ 1 (mod N)
Esto se hace utilizando el algoritmo de estimación de fase cuántica (QPE)
Aprovecha la superposición y el entrelazamiento.
Para encontrar r de manera eficiente.
Una vez encontrado r si r es par y ar/2 ≠ −1 (mod N)
Entonces los factores de N son mcd (ar/2 ± 1, N)
Ejemplo práctico
Supongamos que queremos factorizar N=15
Elegimos a = 7 (aleatorio entre 1 y 15).
Calculamos mcd (7,15) = 1 por lo que procedemos a la parte cuántica.
Usamos QPE para encontrar el orden r de 7 módulo 15.
Supongamos que encontramos r = 4
Como r es par y 74/2 = 49 ≡ 4 (mod 15 ) ≠ −1 calculamos:
Nos da mcd (3,15) = 3 mcd (3,15) = 3 y mcd (5,15) = 5 que son los factores de 15.
Importancia
El algoritmo de Shor demuestra que una computadora cuántica.
Podría romper sistemas criptográficos como RSA.
Ha impulsado la investigación en criptografía post-cuántica.
Algoritmo de Grover
Objetivo
El algoritmo de Grover es un algoritmo cuántico.
De búsqueda en una base de datos no estructurada.
Dado un conjunto de N elementos.
El algoritmo encuentra un elemento específico en O (N) pasos.
En comparación con O (N) pasos en una computadora clásica.
Pasos del algoritmo
El algoritmo de Grover consta de los siguientes pasos:
Inicialización
Se prepara un estado cuántico en superposición uniforme
Oraculo cuántico
Se aplica un oráculo O que marca el estado deseado.
∣ w ⟩ invirtiendo su fase:
Amplificación de amplitud
Se aplica una operación de difusión (Grover diffusion)
Amplifica la amplitud del estado deseado ∣ w ⟩
Reduce las amplitudes de los demás estados.
Iteración
Los pasos 2 y 3 se repiten aproximadamente N veces.
Maximizar la probabilidad de medir el estado deseado.
Medición
Se mide el estado cuántico.
Obteniendo con alta probabilidad el estado deseado ∣ w ⟩
Ejemplo práctico
Supongamos que tenemos una lista no estructurada de 4 elementos (N = 4)
Queremos encontrar el elemento w = 2
Importancia
El algoritmo de Grover es útil en problemas de búsqueda y optimización.
Como la búsqueda en bases de datos.
La resolución de problemas de satisfacción de restricciones.
La optimización combinatoria.
Comparación entre el algoritmo de Shor y el algoritmo de Grover
| Aspecto | Algoritmo de Shor | Algoritmo de Grover |
| Objetivo | Factorizar números enteros grandes | Búsqueda en una base de datos no estructurada |
| Complejidad | O ((logN) 3) ((log) 3) O(N)) | |
| Aplicaciones | Criptografía, teoría de números | Búsqueda, optimización, aprendizaje automático |
| Uso de QPE | Sí (para encontrar el orden) | No |
| Impacto en criptografía | Rompe RSA y otros sistemas basados en factorización | No afecta directamente a la criptografía |
Implementación práctica
Algoritmo de Shor
Se puede implementar en frameworks como Qiskit IBM o Cirq Google.
Ejemplo en Qiskit:
Implementar QPE para encontrar el orden de un número módulo N
Algoritmo de Grover
También se puede implementar en Qiskit o Cirq.
Ejemplo en Qiskit:
Crear un oráculo que marque un estado específico.
Aplicar la iteración de Grover.
El algoritmo de Shor y el algoritmo de Grover
Son dos pilares de la computación cuántica.
Potencial para superar a las computadoras clásicas en tareas específicas.
Shor tiene implicaciones profundas para la criptografía.
Grover es una herramienta poderosa para la búsqueda y la optimización