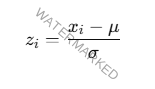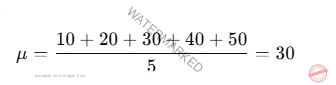Z-score Normalization – Normalización por Puntuación Estándar
La normalización por Z-score también conocida como estandarización
Es una técnica de preprocesamiento utilizada en aprendizaje automático y análisis de datos.
Transforma los valores de un conjunto de datos.
De tal forma que tengan una media de 0 y una desviación estándar de 1.
Este método facilita el análisis de datos.
Mejora el rendimiento de los modelos de aprendizaje automático.
Garantiza que las características tengan la misma escala.
Fórmula de Normalización por Z-score
Escalado de Características
Las características deben estar en la misma escala.
Evitar que características con rangos más amplios.
Dominen el modelo.
Rendimiento de Modelos
La normalización por Z-score mejora la convergencia.
De los algoritmos de optimización.
El descenso de gradiente.
Al reducir la variación en las escalas.
De las características.
Interpretabilidad de los Datos
Los valores normalizados permiten una interpretación.
Más uniforme y comparaciones más claras entre características.
Ejemplo Práctico
Un conjunto de datos con una característica X = [10, 20, 30, 40, 50]
X = [ 10, 20, 30, 40, 50] X = [ 10, 20, 30, 40, 50].
Calculemos su normalización por Z-score.
Cálculo de la Media (μ)
Aplicación en Python
import numpy as np
from sklearn.preprocessing import StandardScaler
# Datos originales
X = np.array([[10], [20], [30], [40], [50]])
# Normalización manual
mean = np.mean(X)
std = np.std(X)
z_scores_manual = (X – mean) / std
print(«Z-scores (manual):», z_scores_manual.flatten())
# Normalización con Scikit-learn
scaler = StandardScaler()
z_scores_sklearn = scaler.fit_transform(X)
print(«Z-scores (Scikit-learn):», z_scores_sklearn.flatten())
Salida esperada
Z-scores (manual): [-1.41 -0.71 0. 0.71 1.41] Z-scores (Scikit-learn): [-1.41 -0.71 0. 0.71 1.41]
Ventajas de la Normalización por Z-score
Elimina la Influencia de Escalas Diferentes
Facilita que los algoritmos se concentren en los patrones.
Inherentes en los datos en lugar de ser influenciados.
Por escalas variables.
Adecuado para Datos Normalmente Distribuidos
Funciona bien cuando las características tienen.
Una distribución normal o aproximadamente normal.
Mejora de Modelos Basados en Distancias
Algoritmos como KNN y SVM.
Dependen de la distancia entre puntos.
Se benefician enormemente de esta normalización.
Desventajas de la Normalización por Z-score
Sensibilidad a Outliers
La media y la desviación estándar son sensibles a valores atípicos.
Puede afectar negativamente el resultado.
No Conserva Rangos Absolutos
Los valores normalizados pierden su relación.
Con las unidades originales.
Puede dificultar la interpretación directa.
La normalización por Z-score es una técnica para preprocesar datos.
Antes de entrenar modelos.
Garantiza que todas las características tengan la misma escala.
Mejora significativamente el rendimiento.
De muchos algoritmos de aprendizaje automático.
Te puede interesar;