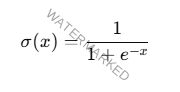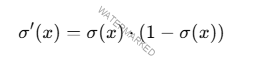Función sigmoide es una función de activación utilizada en redes neuronales.
En las primeras etapas del aprendizaje profundo.
Capacidad para mapear valores reales.
En un rango limitado entre 0 y 1
Útil en tareas de clasificación binaria.
En arquitecturas de salidas probabilísticas.
Definición Matemática
La función sigmoide está definida como:
x es la entrada de la función.
e es el número de Euler.
Propiedades clave
Rango: (0,1) (0, 1) .
Forma: Su gráfico tiene una forma en «S» suave y continua.
Punto de inflexión: Ocurre en x = 0 donde σ (0) = 0.5
Asintotas: Se aproxima a 0 para x → −∞ y a 1 para x → +∞
Derivada de la Función Sigmoide
La derivada de la función sigmoide.
Esta derivada es útil durante el entrenamiento.
De redes neuronales para calcular los gradientes.
Necesarios en la retropropagación.
Ventajas de la Función Sigmoide
Interpretación probabilística
La salida está limitada entre 0 y 1
Puede interpretar como una probabilidad.
En tareas de clasificación binaria.
Una salida cercana a 1 indica una alta probabilidad.
De pertenencia a una clase.
Suavidad
Es una función continua y diferenciable.
En todo su dominio.
Facilita el cálculo de gradientes.
La optimización.
Normalización de salidas
Comprime las entradas en un rango limitado.
Evitando que las activaciones crezcan sin control.
Limitaciones de la Función Sigmoide
Saturación y desvanecimiento del gradiente
Para valores de entrada muy positivos o negativos.
La pendiente de la función se aproxima a cero.
Esto resulta en gradientes pequeños.
Dificultando el aprendizaje en redes profundas.
Problema del desvanecimiento del gradiente.
Rango no centrado en cero
Las salidas de la sigmoide están en el rango (0, 1) (0, 1)
Introduce un sesgo positivo en la propagación.
De los gradientes.
Puede ralentizar el entrenamiento.
Ineficiencia en redes profundas
La sigmoide ha sido reemplazada.
Por funciones como ReLU
En redes neuronales profundas.
Comparación con otras funciones de activación
| Propiedad | Sigmoide | Tanh | ReLU |
|---|---|---|---|
| Rango | (0,1)(0, 1) | (−1,1)(-1, 1) | [0,∞)[0, \infty) |
| Centro | No centrado | Cero | No centrado |
| Saturación | Sí (en valores extremos) | Sí (en valores extremos) | No (para valores >0>0) |
| Gradiente | Desaparece en extremos | Más estable que sigmoide | No desaparece (ReLU) |
Aplicaciones de la Función Sigmoide
Clasificación binaria
En la salida de redes neuronales.
Tareas de clasificación binaria.
Funciones de pérdida como la entropía cruzada.
Regresión logística
La sigmoide se utiliza para mapear valores.
De entrada a probabilidades.
Neuronas individuales
La sigmoide es una opción para las activaciones.
De las capas ocultas.
Ejemplo de uso en Python
En un modelo secuencial de Keras.
Se utiliza en la capa de salida.
Tareas de clasificación binaria:
from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import Dense
# Definir un modelo con función sigmoide
model = Sequential([
Dense(32, activation=’relu’, input_shape=(100,)),
Dense(1, activation=’sigmoid’) # Salida con activación sigmoide
])
# Compilar el modelo
model.compile(optimizer=’adam’, loss=’binary_crossentropy’, metrics=[‘accuracy’])
# Entrenamiento
# model.fit(X_train, y_train, epochs=10, batch_size=32)
Te puede interesar;
