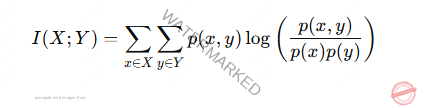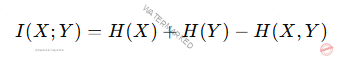La información mutua es un concepto fundamental en teoría de la información.
Y aprendizaje automático que mide la dependencia estadística.
Entre dos variables aleatorias.
Proporciona una manera cuantitativa.
De saber cuánta información comparte una variable sobre otra.
Cuánto saber una variable reduce la incertidumbre acerca de la otra.
En el contexto de la IA se utiliza principalmente para evaluar relaciones.
Entre características y etiquetas.
Para la selección de características y modelado.
De dependencias en datos complejos.
Definición Formal
La información mutua I (X; Y) entre dos variables aleatorias X y Y se define como;
Donde:
p (x,y) es la probabilidad conjunta de que X = x y Y = y.
p(x) y p(y) son las probabilidades marginales de XXX y YYY respectivamente.
La unidad de medida depende del logaritmo utilizado.
Se expresa en bits si se usa el logaritmo base 2
En nats si se usa el logaritmo natural.
Intuición y Propiedades
Medición de dependencia
Si I (X; Y) = 0, las variables X y Y son completamente independientes
Conocer una no proporciona ninguna información sobre la otra.
Valores más altos de I(X;Y)I(X; Y)I(X;Y) indican una mayor dependencia entre las variables.
Simetría
La información mutua es simétrica: I (X; Y) = I (Y; X)
Esto significa que la cantidad de información que X
proporciona sobre Y
Es la misma que la que Y proporciona sobre X.
Relación con la entropía
La información mutua puede expresarse en términos de la entropía (H)
Mide la incertidumbre de una variable:
Esto ilustra que la información mutua refleja la reducción conjunta.
De incertidumbre al conocer ambas variables.
Aplicaciones en IA y Machine Learning
Selección de características
Se utiliza para identificar las características más relevantes.
Que tienen mayor relación informativa con la variable objetivo.
Ayuda a reducir la dimensionalidad del espacio de entrada.
Mejorando la eficiencia del modelo.
Análisis de relaciones entre variables
Se emplea para entender cómo las variables de entrada.
Se relacionan entre sí y con la salida.
Informando decisiones de ingeniería.
De características y modelado.
Modelos gráficos probabilísticos
En el modelado de redes bayesianas o gráficos probabilísticos.
La información mutua permite determinar las dependencias.
Condicionales y estructuras de relaciones.
Entre variables aleatorias.
Procesamiento del lenguaje natural (NLP)
Se puede usar para medir la co-ocurrencia.
Dependencia entre palabras.
Ayudando a la extracción de características.
Para tareas de clasificación de texto.
Modelado del lenguaje.
Segmentación y reconocimiento de imágenes
En la visión por computadora.
Se utiliza para evaluar la correspondencia.
Alineación de imágenes al cuantificar la relación informativa.
Entre distintos puntos o regiones.
Ejemplo Práctico: Selección de Características
En un conjunto de datos de clasificación.
Con múltiples variables de entrada.
La información mutua entre cada variable.
De entrada y la salida se puede calcular.
Para seleccionar solo aquellas con la mayor relación informativa.
Elimina características irrelevantes o redundantes.
Mejorando el rendimiento y reduciendo el tiempo de cómputo del modelo.
Ejemplo:
Dado un conjunto de datos con características X1, X2, …, Xn
Una etiqueta Y, se calcula I (Xi; Y) para cada característica Xi.
Se seleccionan las características con los valores más altos.
De información mutua.
Limitaciones
Sensibilidad al tamaño del conjunto de datos
La estimación de probabilidades conjuntas.
Puede ser poco confiable si el conjunto de datos es pequeño.
Afecta la precisión del cálculo de la información mutua.
Dificultad con variables continuas
Para variables continuas.
La información mutua requiere una discretización adecuada.
Métodos de estimación complejos.
No captura dependencias no lineales complejas
Si bien es una medida general de dependencia.
Puede no captar relaciones no lineales.
Intrincadas que otros métodos especializados pueden detectar.
La información mutua es una herramienta valiosa en IA y aprendizaje automático.
Entender la dependencia y relación entre variables.
Su aplicación es fundamental en la selección de características.
Análisis de relaciones y modelado probabilístico.
Siendo una medida robusta aunque limitada.
Por la calidad y cantidad de los datos disponibles.
Te puede interesar;