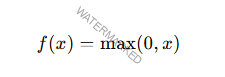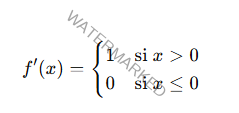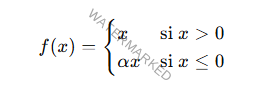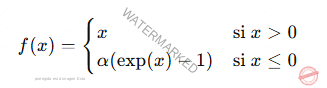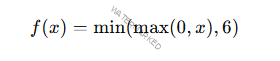ReLU (Rectified Linear Unit) es una función de activación.
Utilizada en redes neuronales artificiales.
En arquitecturas profundas (Deep Learning).
Introducida como una alternativa eficiente.
Computacionalmente económica a funciones.
La sigmoide o la tangente hiperbólica.
ReLU ha revolucionado el aprendizaje profundo.
Acelera el entrenamiento de modelos.
Mejorar su desempeño.
Definición Matemática
La función ReLU se define;
Esto significa que la salida de ReLU.
Igual al valor de entrada x si x> 0x > 0x > 0
Igual a 0 si x ≤ 0x
Gráficamente la función es lineal para valores positivos.
Constante (cero) para valores negativos.
Propiedades Clave
No Linealidad por Tramos
Aunque la función es lineal para x > 0x > 0x > 0
La inclusión de una «interrupción» en x = 0x = 0x = 0
No linealidad necesaria para modelar.
Relaciones complejas en los datos.
Computación Eficiente
Su simplicidad matemática la hace extremadamente rápida.
De calcular solo implica comparar valores.
Realizar una operación básica de máximo.
Sparsity (Esparsidad)
ReLU activa solo un subconjunto de las neuronas en la red.
Aquellas con valores positivos.
Introduce esparsidad reduce la sobrecarga
Computacional y mejora la eficiencia.
Derivabilidad
La derivada de ReLU
Aunque no está definida en x = 0x = 0x = 0
No afecta significativamente el entrenamiento.
Ventajas de ReLU
Resolución del Problema de Desvanecimiento del Gradiente
Las funciones como la sigmoide y la tangente.
Hiperbólica tienden a «aplanar» los gradientes en sus extremos.
Dificultando el entrenamiento en redes profundas.
ReLU al mantener valores lineales para x > 0x > 0x > 0
Evita este problema.
Convergencia Rápida
Dado que la función es lineal en valores positivos.
Facilita la propagación de gradientes grandes.
Durante el entrenamiento.
Acelera la convergencia.
Simplicidad Computacional
La implementación de ReLU es sencilla y eficiente.
En hardware y software.
Ideal para redes grandes.
Promueve Esparsidad
ReLU desactiva neuronas (salida = 0)
Para entradas negativas introduce esparsidad.
Puede ayudar a evitar el sobreajuste.
Mejora la interpretabilidad de la red.
Limitaciones de ReLU
Neurona Muerta (Dying Neuron Problem)
Si durante el entrenamiento muchas entradas producen valores negativos.
Las neuronas correspondientes se «apagan» permanentemente.
Sus gradientes serán cero.
Esto puede llevar a una pérdida de capacidad de aprendizaje.
No Apta para Valores Negativos
ReLU descarta toda la información negativa.
Podría ser problemático en algunos contextos.
Donde estos valores son significativos.
Variantes de ReLU
Para abordar las limitaciones de la función estándar
Leaky ReLU
Introduce un pequeño gradiente para valores negativos.
Donde α es un pequeño valor positivo (típicamente 0.01)
Parametric ReLU (PReLU)
Similar a Leaky ReLU, pero α se aprende durante el entrenamiento.
Exponential Linear Unit (ELU)
Introduce una curva suave para valores negativos:
Scaled Exponential Linear Unit (SELU)
Una versión normalizada de ELU.
Diseñada para mantener la activación en un rango.
Adecuado en redes profundas.
ReLU6
Similar a ReLU, pero con un límite superior de 6
Común en arquitecturas optimizadas.
Hardware como MobileNet.
Aplicaciones de ReLU
ReLU es fundamental en muchas arquitecturas de redes neuronales.
Redes Convolucionales (CNNs)
ReLU se utiliza ampliamente después de las capas convolucionales.
Introducir no linealidad y reducir la computación.
Redes Recurrentes (RNNs)
ReLU puede ser útil en variantes como LSTM o GRU.
Redes Profundas
Es la función de activación predeterminada.
En arquitecturas como AlexNet, VGG y ResNet.
Debido a su simplicidad y efectividad.
Procesamiento de Imágenes y Videos
ReLU ayuda a capturar características complejas al procesar datos visuales.
ReLU es una función de activación que ha demostrado ser simple.
Eficiente y efectiva en una amplia variedad de tareas.
Su capacidad para mitigar el problema del desvanecimiento.
Del gradiente y facilitar el entrenamiento de redes profundas.
Las variantes de ReLU amplían su aplicabilidad.
Ofrecen soluciones robustas en casos específicos.
Te puede interesar;