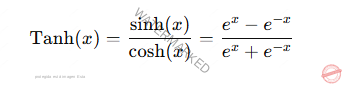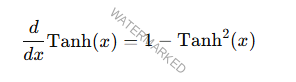La función tangente hiperbólica Tanh es una función de activación.
Utilizada en redes neuronales artificiales.
En arquitecturas más antiguas y en redes recurrentes (RNNs).
Capacidad para manejar entradas normalizadas.
Proporcionar una activación no lineal.
Facilita el aprendizaje de relaciones complejas en los datos.
Definición Matemática
La función Tanh está definida.
Propiedades clave
Rango de valores: (−1, 1) (-1, 1) (−1, 1)
Es simétrica respecto al origen es una función impar.
Valores grandes positivos Tanh se aproxima a 1.
Valores grandes negativos Tanh se aproxima a −1.
Derivada de Tanh
La derivada de Tanh se calcula como:
Es útil en el cálculo de gradientes.
Durante el entrenamiento de redes neuronales.
Permite ajustar los pesos de forma eficiente.
Ventajas de Tanh
Rango Centrado en Cero
La función sigmoide cuyo rango es [0,1] [0, 1] [0,1]
El rango de Tanh está centrado en cero (−1, 1) (-1, 1) (−1, 1)
Facilita el aprendizaje en redes neuronales.
La activación no está sesgada.
Hacia valores positivos.
Normalización de Salidas
La función Tanh comprime las entradas.
En un rango limitado.
Ayuda a estabilizar el entrenamiento.
Evita que las activaciones se disparen.
Capacidad de Modelar Relaciones No Lineales
Tanh introduce no linealidad.
Permite a las redes neuronales aprender.
Relaciones complejas en los datos.
Uso en Redes Recurrentes (RNNs)
Capacidad para manejar valores normalizados.
Es crítico al procesar secuencias.
Limitaciones de Tanh
Desvanecimiento del Gradiente
En valores extremos muy positivos o muy negativos.
Las salidas de Tanh se saturan.
Cerca de 1 o −1 -1 −1
Los gradientes tienden a ser muy pequeños.
Puede dificultar el aprendizaje en redes profundas.
Costos Computacionales
ATanh es computacionalmente más exigente que ReLU.
debido a la necesidad de calcular exponentes.
Comparación con otras funciones de activación
| Propiedad | Tanh | Sigmoide | ReLU |
|---|---|---|---|
| Rango | (−1,1)(-1, 1)(−1,1) | (0,1)(0, 1)(0,1) | [0,∞)[0, \infty)[0,∞) |
| Centro | Cero | No centrado | No centrado |
| Saturación | Sí (en valores extremos) | Sí (en valores extremos) | No (para valores >0>0>0) |
| Gradiente | Más estable que sigmoide | Propenso a desvanecerse | No desaparece (ReLU) |
Aplicaciones de Tanh
Redes Neuronales Recurrentes (RNNs)
Capacidad para manejar valores normalizados,
Tanh es ampliamente utilizada en capas recurrentes.
Modelos como LSTM y GRU.
Redes Neuronales Multicapa (MLP)
Tanh se utilizaba para introducir no linealidad.
Antes de la llegada de ReLU.
Tareas de Clasificación
Cuando las salidas de las capas intermedias.
Necesitan estar centradas en cero.
Tanh es una elección natural.
Procesamiento de Señales y Secuencias
Tanh es útil para suavizar y normalizar señales.
En tareas como análisis de series temporales.
Generación de texto.
Ejemplo de uso en una red neuronal
En un modelo secuencial de Keras.
Puede usar Tanh como función de activación.
En cualquier capa densa o recurrente.
from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import Dense
# Modelo secuencial simple
model = Sequential([
Dense(64, activation=’tanh’, input_shape=(100,)),
Dense(1, activation=’sigmoid’)
])
# Compilación del modelo
model.compile(optimizer=’adam’, loss=’binary_crossentropy’)
En este ejemplo, Tanh se utiliza en una capa oculta para proporcionar activaciones centradas en cero.
La función Tanh es una herramienta valiosa en el aprendizaje profundo.
En arquitecturas donde la normalización de valores.
La simetría en las activaciones son críticas.
Aunque ha sido en gran medida reemplazada.
Por funciones como ReLU en redes profundas.
Tanh sigue siendo una opción en redes recurrentes.
Adecuada para tareas donde el centrado en cero es esencial.
Te puede interesar;